- El Muro Invisible: ¿Por Qué el Cálculo es Decisivo en tu Examen?
- Fundamentos Sólidos: La Base Oculta en la que Todos Tropiezan
- La Derivada: El Corazón del Cálculo y tu Pasaporte a Ingeniería
- Aplicaciones de la Derivada: Donde Demuestras que Serás Ingeniero
- Mentalidad de Campeón: Cómo Enfrentar el Examen sin Pánico
- Tu Futuro Empieza Ahora
Respira hondo.
Sientes esa mezcla de emoción y pánico, ¿verdad? La palabra "INGENIERÍA" resuena en tu cabeza con la fuerza de una promesa. Un futuro construyendo, creando, innovando.
Pero hay un guardián en la puerta de ese futuro. Un dragón que debes vencer.
Se llama Cálculo Diferencial.
Para muchos, es la materia que separa a los aspirantes de los admitidos. Un filtro diseñado para medir no solo si sabes una fórmula, sino cómo piensas.
La buena noticia es que no estás solo en esto. Y este no es otro aburrido post con una lista de temas.
Esta es tu nueva arma secreta.
Aquí no solo te voy a enseñar a resolver los problemas. Te voy a enseñar a desmontarlos, a verles las costuras, a entender la lógica que tu examinador usó para crearlos. Te voy a mostrar los reactivos clave, esos que se repiten año tras año en diferentes formas, y te daré los trucos y atajos mentales que tu competencia desearía conocer.
¿El objetivo? Que cuando abras tu examen de admisión, sonrías. Que sientas la calma del que va preparado para la batalla porque ya la ha peleado —y ganado— decenas de veces en su mente.
Olvídate de memorizar sin entender. Hoy vas a aprender a pensar como un ingeniero. Y todo empieza aquí.
El Muro Invisible: ¿Por Qué el Cálculo es Decisivo en tu Examen?
Antes de lanzarnos a las ecuaciones, seamos brutalmente honestos. El cálculo diferencial no está en tu examen para hacerte la vida imposible (aunque a veces lo parezca). Está ahí por una razón fundamental: la ingeniería es el estudio del cambio.
- ¿Cómo cambia la velocidad de un cohete al consumir combustible? Eso es una derivada.
- ¿Cómo diseñar una viga para que soporte el máximo peso con el mínimo material? Eso es optimización con derivadas.
- ¿Cómo varía el voltaje en un circuito a lo largo del tiempo? Eso es una razón de cambio.
El cálculo es el lenguaje que describe el movimiento, la velocidad, la aceleración y la optimización. Es la base sobre la que construirás todo tu conocimiento como ingeniero. Tu examen de admisión no está evaluando si puedes ser un buen ingeniero mañana, está evaluando si tienes la herramienta mental básica para empezar a serlo.
Entender esto cambia el juego. No estás estudiando para pasar un examen. Estás afilando la herramienta más importante de tu futura carrera.
Ahora sí, vamos a afilarla.
Fundamentos Sólidos: La Base Oculta en la que Todos Tropiezan
Imagina que quieres construir un rascacielos. ¿Empezarías por el piso 50? No. Empezarías por una cimentación tan profunda y robusta que nadie la ve, pero que sostiene todo el edificio. En cálculo, esa cimentación son las funciones y los límites.
Muchos saltan esto para ir directo a "lo bueno" (las derivadas) y ahí es donde cometen su primer gran error. El 90% de los fallos en problemas de derivadas no son por la derivada en sí, ¡son por un álgebra deficiente o una mala comprensión de los límites!
Tema Clave 1: Límites, el Arte de Acercarse sin Tocar
Un límite te dice a qué valor se acerca una función (\(y\)) cuando la variable (\(x\)) se acerca a un número específico. Simple, ¿no? Pero es la base de toda la continuidad y, más importante, de la propia definición de derivada.
Tu examen no te pondrá un límite fácil que solo se resuelve sustituyendo. Eso es un regalo y los examinadores no son tan generosos. Buscarán probar tu habilidad en los casos donde las cosas se "rompen".
Long-tail a atacar: "cómo resolver límites indeterminados para examen de admisión"
Los límites que te encontrarás serán, en su mayoría, indeterminados. Es decir, que al sustituir el valor de \(x\) te darán cosas como \(\frac{0}{0}\) o \(\frac{\infty}{\infty}\). Estas son señales. No significan "no existe", significan "trabaja más, futuro ingeniero".
Tus herramientas para destruir indeterminaciones:
- Factorización: Tu mejor amigo del álgebra. Si tienes polinomios arriba y abajo, es casi seguro que hay un factor \((x - a)\) escondido que puedes cancelar.
- Racionalización: Si ves una raíz cuadrada, especialmente en una resta, multiplica arriba y abajo por el conjugado. Es como magia.
- Límites al Infinito: Divide todo (numerador y denominador) entre la potencia más alta de \(x\) que veas en el denominador. Todo lo que quede como \(\frac{\text{constante}}{\infty}\) se irá a cero.
Reactivo Clave de Examen: Límite con Factorización
\(\lim_{x \to 2} \frac{x^2 - 4}{x^2 - 5x + 6}\)Calcula el siguiente límite:
Análisis Previo (Mentalidad de Ingeniero):
- Sustituyo \(x = 2\).
- Numerador: \(2^2 - 4 = 4 - 4 = 0\).
- Denominador: \(2^2 - 5(2) + 6 = 4 - 10 + 6 = 0\).
- Resultado: \(\frac{0}{0}\). ¡Indeterminado! Esto es una pista, no una barrera. El examen me está diciendo que el factor \((x - 2)\) está causando el problema y debo eliminarlo.
Solución Paso a Paso (A prueba de errores):
- Identifica la indeterminación: Ya lo hicimos, es \(\frac{0}{0}\). Esto valida que debemos seguir trabajando.
- Factoriza el numerador: Es una diferencia de cuadrados. Fácil.
Factoriza el denominador: Es un trinomio. Buscamos dos números que multiplicados den +6 y sumados den -5. Esos son -2 y -3.
Reescribe y simplifica el límite: Ahora volvemos a montar la fracción con los factores.
\(\lim_{x \to 2} \frac{(x - 2)(x + 2)}{(x - 2)(x - 3)}\)¡Ahí está! El factor \((x - 2)\) que causaba los ceros. Lo cancelamos.
\(\lim_{x \to 2} \frac{x + 2}{x - 3}\)Evalúa el límite simplificado: Ahora sí, sustituimos \(x = 2\) sin miedo.
Esto también puede interesarte...
El Error Común: Dejarse intimidar por el \(\frac{0}{0}\) y marcar "no existe" o "es infinito". Recuerda: \(\frac{0}{0}\) es una invitación a simplificar.
El Truco del Experto: Cuando sepas que el límite tiende a \(a\) y te da \(\frac{0}{0}\), ya sabes que \((x - a)\) SERÁ un factor en ambos polinomios. No tienes que "buscar" los factores, ya sabes cuál es uno de ellos. Esto te ahorra tiempo y estrés.
La Derivada: El Corazón del Cálculo y tu Pasaporte a Ingeniería
Si los límites son la base, la derivada es el primer gran pilar. Y aquí es donde el examen sube de nivel.
En español simple: La derivada de una función en un punto es la pendiente de la recta tangente a la gráfica en ese punto. También representa la razón de cambio instantánea.
Piensa en un coche. Su velocidad promedio es la distancia total entre el tiempo total. Su velocidad instantánea (la que ves en el velocímetro) es la derivada de su posición en ese preciso instante. Los ingenieros viven de lo instantáneo.
Tu examen atacará las derivadas desde tres ángulos:
- Definición formal (límite): Menos común, pero puede aparecer para filtrar a los que solo memorizan fórmulas.
- Reglas de derivación: El pan de cada día. Aquí es donde debes ser una máquina.
- Interpretación y aplicaciones: El nivel más alto. Te dan un problema del "mundo real" y tú debes modelarlo con derivadas.
Tema Clave 2: Las Reglas de Derivación que Debes Dominar como tu Nombre
Long-tail a atacar: "reglas de derivación para examen de ingreso ingeniería"
No hay atajos aquí. Debes conocer estas reglas a la perfección. La clave no es solo memorizarlas, sino reconocer CUÁNDO usar cada una.
- Regla de la Potencia: La más básica. Si \(f(x) = x^n\), entonces \(f'(x) = nx^{n-1}\).
- Regla del Producto: Para derivar \(f(x) \cdot g(x)\). La fórmula es \((f'g + fg')\).
- Regla del Cociente: Para derivar \(\frac{f(x)}{g(x)}\). La fórmula es \(\frac{f'g - fg'}{g^2}\).
- Derivadas Trigonométricas: Debes saber de memoria la derivada de \(\sin(x)\), \(\cos(x)\), \(\tan(x)\), etc.
Pero la reina de todas, la que aparece en el 80% de los problemas complejos, es...
Tema Clave 3: La Regla de la Cadena, Tu Arma Definitiva
Long-tail a atacar: "regla de la cadena ejercicios para examen de ingreso"
La regla de la cadena se usa cuando tienes una función dentro de otra función (una función compuesta). Ejemplo: \(y = \sin(x^2)\) o \(y = \sqrt{4x+1}\).
La analogía infalible: La Matrioshka (muñeca rusa) Imagina que tienes una de esas muñecas rusas. Para llegar a la más pequeña, tienes que abrir la de afuera primero. La regla de la cadena es igual:
Deriva la función de afuera (dejando lo de adentro intacto) y luego multiplica por la derivada de la función de adentro.
Reactivo Clave de Examen: Derivada con Regla de la Cadena y Producto
\(f(x) = x^3 \cdot \cos(5x^2)\)Encuentra la derivada de la función:
Análisis Previo (Mentalidad de Ingeniero):
- Veo dos partes principales multiplicándose: \(x^3\) y \(\cos(5x^2)\). Esto grita Regla del Producto.
- La segunda parte, \(\cos(5x^2)\), no es simple. Es una función (
coseno) con otra función adentro (\(5x^2\)). Esto grita Regla de la Cadena. - El problema es una combinación. Debo aplicar la Regla del Producto globalmente, y DENTRO de uno de sus pasos, tendré que usar la Regla de la Cadena.
Solución Paso a Paso (Desglosando la bestia):
- Define tus partes para la Regla del Producto:
Deriva la primera parte (fácil):
- \(u'(x) = 3x^2\) (Regla de la Potencia)
Deriva la segunda parte (el reto): Aquí usamos la Regla de la Cadena para \(v(x) = \cos(5x^2)\).
- Función de afuera: \(\cos(\text{algo})\)
- Función de adentro: \(5x^2\)
- Derivada de la de afuera: La derivada de \(\cos(\text{algo})\) es \(-\sin(\text{algo})\).
- \(-\sin(5x^2)\) (dejamos lo de adentro intacto)
- Derivada de la de adentro: La derivada de \(5x^2\) es \(10x\).
- Júntalo todo (multiplica): \(v'(x) = -\sin(5x^2) \cdot (10x) = -10x \sin(5x^2)\)
Aplica la fórmula de la Regla del Producto (\(u'v + uv'\)): Ahora tienes todas las piezas. Solo tienes que ensamblarlas con cuidado.
\(f'(x) = (3x^2) \cdot (\cos(5x^2)) + (x^3) \cdot (-10x \sin(5x^2))\)Simplifica y presenta el resultado final:
\(f'(x) = 3x^2 \cos(5x^2) - 10x^4 \sin(5x^2)\)El Error Común: Olvidar aplicar la Regla de la Cadena. Muchos derivan \(\cos(5x^2)\) como \(-\sin(5x^2)\) y se olvidan de multiplicar por la derivada de lo de adentro (\(10x\)). El examinador PONE esa respuesta incorrecta en las opciones para atraparte.
El Truco del Experto: Siempre que derives, pregúntate: ¿la variable \(x\) está "sola" o está siendo "afectada" por algo más? Si es \(\sin(x)\), la \(x\) está sola. Si es \(\sin(5x^2)\), la \(x\) está siendo elevada al cuadrado y multiplicada por 5. Esa es tu señal para usar la Regla de la Cadena.
Aplicaciones de la Derivada: Donde Demuestras que Serás Ingeniero
Aquí es donde se separa la élite. Las aplicaciones son problemas de texto. No te dan la función, no te dan la ecuación. Te dan un escenario. Tu trabajo es traducir ese escenario al lenguaje del cálculo, resolverlo y luego traducir la respuesta de vuelta al contexto del problema.
Esto es 100% pensamiento de ingeniero.
Tema Clave 4: Razón de Cambio, el Mundo en Movimiento
Long-tail a atacar: "problemas de razón de cambio para examen de admisión"
Estos problemas involucran variables que cambian con el tiempo. La clave siempre es encontrar una ecuación que relacione las variables estáticas y luego derivarla implícitamente con respecto al tiempo (\(t\)).
Reactivo Clave de Examen: El Clásico de la Escalera
Una escalera de 10 metros de largo está apoyada contra una pared vertical. La base de la escalera se resbala, alejándose de la pared a una velocidad constante de 2 m/s. ¿Con qué velocidad se desliza hacia abajo la parte superior de la escalera cuando la base está a 6 metros de la pared?
Análisis Previo (Mentalidad de Ingeniero):
- Dibujo: Lo primero es dibujar un triángulo rectángulo. La hipotenusa es la escalera (longitud constante = 10). Un cateto es la distancia de la base a la pared (lo llamaré \(x\)). El otro cateto es la altura en la pared (lo llamaré \(y\)).
- ¿Qué sé? (Datos):
- Longitud de la escalera = 10 m (constante)
- Velocidad a la que se aleja la base: \(\frac{dx}{dt} = 2\) m/s (es positiva porque \(x\) aumenta).
- Posición en un instante específico: \(x = 6\) m.
- ¿Qué busco? (Incógnita):
- La velocidad a la que baja la parte superior: \(\frac{dy}{dt}\) en el instante en que \(x = 6\). Espero que sea negativa, porque \(y\) está disminuyendo.
- La Ecuación Maestra: ¿Qué relaciona a \(x\), \(y\) y 10? ¡El Teorema de Pitágoras! \(x^2 + y^2 = 10^2\).
Solución Paso a Paso (Traduciendo el mundo real a matemáticas):
- Establece la ecuación que relaciona las variables:
Deriva TODA la ecuación implícitamente con respecto al tiempo (\(t\)): Recuerda usar la regla de la cadena para cada variable.
Esto también puede interesarte...
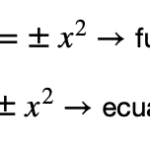
Encuentra los valores que te faltan para el instante específico:
- Sabemos que \(x=6\).
- Sabemos que \(\frac{dx}{dt} = 2\).
- Buscamos \(\frac{dy}{dt}\).
- Nos falta \(y\). ¿Cómo la encontramos? Usamos la ecuación estática original (\(x^2 + y^2 = 100\)) para ese instante.
Sustituye todo en la ecuación derivada y despeja tu incógnita:
\(2(6)(2) + 2(8) \frac{dy}{dt} = 0\)\(24 + 16 \frac{dy}{dt} = 0\)\(16 \frac{dy}{dt} = -24\)\(\frac{dy}{dt} = -\frac{24}{16} = -\frac{3}{2} = -1.5 \text{ m/s}\)Interpreta el resultado: La parte superior de la escalera se desliza hacia abajo (el signo negativo lo confirma) a una velocidad de 1.5 m/s en ese preciso instante.
El Error Común: Sustituir el valor de \(x=6\) ANTES de derivar. Si haces eso, tratas a \(x\) como una constante y su derivada sería cero, lo cual arruina todo el problema. Recuerda: primero derivas la fórmula general, LUEGO sustituyes los valores del instante.
El Truco del Experto: Identifica siempre qué cantidades son variables y cuáles son constantes. La longitud de la escalera es constante. Las distancias \(x\) e \(y\) y sus velocidades son variables. Esta distinción es crucial.
Tema Clave 5: Optimización, el Superpoder del Ingeniero
Long-tail a atacar: "cómo resolver problemas de optimización con derivadas"
La optimización consiste en encontrar el valor máximo o mínimo de una función bajo ciertas condiciones. Maximizar ganancias, minimizar costos, maximizar el volumen, minimizar el material. Esto es la ingeniería en su estado más puro.
La Receta Universal para Problemas de Optimización:
- Entender el Objetivo: ¿Qué te piden maximizar o minimizar? Esa será tu función objetivo.
- Identificar la Restricción: ¿Qué te limita? El material disponible, un perímetro fijo, etc. Esta será tu ecuación de restricción.
- Poner la Función Objetivo en Términos de UNA Sola Variable: Usa la ecuación de restricción para despejar una variable y sustituirla en la función objetivo.
- Derivar e Igualar a Cero: Encuentra la derivada de tu función objetivo de una sola variable y encuentra los puntos críticos (donde la derivada es 0 o no existe).
- Verificar si es Máximo o Mínimo: Usa el criterio de la primera o la segunda derivada para confirmar.
Reactivo Clave de Examen: La Caja de Cartón
Se quiere construir una caja sin tapa a partir de una lámina de cartón de 16 cm de ancho por 30 cm de largo, cortando cuadrados iguales en cada esquina y doblando los lados. ¿Cuál debe ser la longitud del lado de los cuadrados cortados para que el volumen de la caja sea máximo?
Análisis Previo (Mentalidad de Ingeniero):
- Objetivo: Maximizar el Volumen de la caja. Mi función objetivo será \(V = \text{largo} \cdot \text{ancho} \cdot \text{alto}\).
- Visualización: Imagino la lámina. Si corto un cuadrado de lado \(x\) en cada esquina, la altura de la caja al doblarla será \(x\). El nuevo largo no será 30, será \(30 - 2x\) (quito \(x\) de cada lado). El nuevo ancho será \(16 - 2x\).
- Función Objetivo en una variable: Ya tengo todo en términos de \(x\).
- Alto: \(h = x\)
- Largo: \(l = 30 - 2x\)
- Ancho: \(a = 16 - 2x\)
Solución Paso a Paso (Construyendo la solución):
- Define la función a optimizar:
Primero, expandimos esto para poder derivarlo fácilmente:
\(V(x) = (480 - 60x - 32x + 4x^2)x\)\(V(x) = (4x^2 - 92x + 480)x\)\(V(x) = 4x^3 - 92x^2 + 480x\)Define el dominio práctico: \(x\) debe ser mayor que 0. Y no puedo cortar más de la mitad del lado más corto, así que \(2x\) debe ser menor que 16, lo que implica \(x < 8\). Dominio: \((0, 8)\).
Deriva la función:
\(V'(x) = 12x^2 - 184x + 480\)Iguala la derivada a cero y resuelve para \(x\):
\(12x^2 - 184x + 480 = 0\)Podemos simplificar dividiendo todo entre 4:
\(3x^2 - 46x + 120 = 0\)Esto no factoriza fácil, así que usamos la fórmula cuadrática:
\(x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\)\(x = \frac{46 \pm \sqrt{(-46)^2 - 4(3)(120)}}{2(3)}\)\(x = \frac{46 \pm \sqrt{2116 - 1440}}{6}\)\(x = \frac{46 \pm \sqrt{676}}{6}\)\(x = \frac{46 \pm 26}{6}\)Esto nos da dos posibles soluciones:
\(x_1 = \frac{46 + 26}{6} = \frac{72}{6} = 12\)\(x_2 = \frac{46 - 26}{6} = \frac{20}{6} = \frac{10}{3} \approx 3.33\)Verifica la solución: Nuestro dominio era \((0, 8)\). La solución \(x=12\) está fuera del dominio, es imposible cortar cuadrados de 12 cm de lado. La única solución válida es \(x = \frac{10}{3}\). El criterio de la segunda derivada (\(V''(x) = 24x - 184\)) sería negativo para \(x=10/3\), confirmando que es un máximo.
Respuesta Final: El lado del cuadrado a cortar debe ser de \(\frac{10}{3}\) cm para obtener el máximo volumen.
El Error Común: No verificar las soluciones contra el dominio práctico del problema. La matemática te puede dar dos respuestas, pero solo una tiene sentido en el mundo real.
El Truco del Experto: Antes de empezar a calcular, dibuja. Visualiza. Entiende las restricciones físicas. Esto te guiará y te ayudará a descartar respuestas ilógicas al final.
Mentalidad de Campeón: Cómo Enfrentar el Examen sin Pánico
Has visto los reactivos, tienes las herramientas. Pero el día del examen, tu peor enemigo no es el cálculo. Es tu propia mente.
- Lee TODO el problema primero: No te lances a calcular al ver el primer número. Entiende la pregunta. ¿Qué te piden exactamente? ¿La velocidad? ¿La posición? ¿El valor máximo? ¿El valor de \(x\) que da el máximo? Son cosas distintas.
- Gestiona tu tiempo: Si un problema se ve monstruoso, márcalo y sigue. Es mejor asegurar 5 preguntas "fáciles" que atascarte 15 minutos en una sola. Ya volverás por ella con la confianza de tener puntos en el bolsillo.
- Confía en las Pistas: Si te da \(\frac{0}{0}\), ¡alégrate! Es una pista para factorizar. Si el problema habla de "velocidad", "razón" o "aumenta/disminuye", ¡alégrate! Es una pista para usar derivadas de razón de cambio. Cada tipo de problema tiene su firma. Aprende a reconocerlas.
- La Respuesta está en las Opciones: En un examen de opción múltiple, a veces puedes usar las respuestas a tu favor. ¿Puedes descartar algunas por ser ilógicas (un tiempo negativo, una longitud mayor a la inicial)? A veces, incluso sustituir una respuesta en el problema es más rápido que resolverlo desde cero.
Tu Futuro Empieza Ahora
Este post es largo. Y denso. Si has llegado hasta aquí, ya has demostrado tener la tenacidad que se necesita.
El cálculo diferencial no es un monstruo invencible. Es un sistema lógico, un lenguaje con reglas claras. Tu trabajo no es tenerle miedo, es desarmarlo pieza por pieza hasta que lo domines.
Guarda esta guía. Practica estos reactivos una y otra vez. Busca variaciones. Explícaselos a un amigo. El que enseña, aprende dos veces.
La plaza en la facultad de ingeniería no es para el que nace sabiendo. Es para el que se prepara con inteligencia, estrategia y una voluntad inquebrantable.
Esto también puede interesarte...

Con esta guía, ya no eres un simple aspirante. Eres un competidor serio.
Ahora, ve y demuestra de qué estás hecho. Tu futuro como ingeniero te está esperando.
Si quieres conocer otros artículos parecidos a Cálculo Diferencial para tu Examen de Admisión a Ingeniería: La Guía Definitiva que tu Competencia NO Quiere que Leas puedes visitar la categoría Guías de Examen de Admisión.
Deja un comentario


Más sobre este tema