Cómo Resolver Problemas de Geometría Analítica Bajo Presión en tu Prueba de Selección

La palabra "Geometría Analítica" en el temario de tu examen de admisión puede sentirse como una sentencia. Ves ecuaciones largas, gráficas confusas y un montón de fórmulas que parecen imposibles de memorizar. En la calma de tu cuarto, quizás logras resolver un problema. Pero, ¿bajo la presión del reloj, con tu futuro en juego? Ahí es donde el pánico ataca.

Respira.

¿Y si te dijera que la Geometría Analítica es la sección más predecible de tu examen? ¿Que no se trata de ser un genio matemático, sino de tener un plan de ataque, un pequeño conjunto de herramientas y la estrategia para saber cuál usar?

Olvídate de memorizar sin sentido. Olvídate de quedarte en blanco frente a una pregunta sobre una elipse. Este no es un formulario, es un manual de combate. Aquí te enseñaremos a desmantelar cada problema, a pensar con claridad bajo presión y a usar el propio examen a tu favor para asegurar esos puntos que definirán tu ingreso.

Prepárate para transformar la ansiedad en confianza.

La Regla de Oro que lo Cambia TODO: Dibuja, Etiqueta, Conecta

Si solo puedes llevarte una cosa de esta guía, que sea esta: la mayoría de los problemas de geometría analítica se resuelven solos si haces un buen dibujo.

El 99% de los errores no ocurren en el álgebra compleja, sino en la interpretación inicial del problema. Tu cerebro procesa información visual millones de veces más rápido que el texto abstracto.

Cálculo Diferencial para tu Examen de Admisión a Ingeniería: La Guía Definitiva que tu Competencia NO Quiere que Leas

1. Dibuja: Incluso si es un boceto rápido y feo en tu hoja de borrador. Dibuja un plano cartesiano. Pon los puntos. Esboza la recta o la curva.
2. Etiqueta: Escribe las coordenadas que conoces. Anota los datos del problema directamente en el dibujo. ¿Te dan un radio? Escríbelo. ¿Una pendiente? Anótala.
3. Conecta: Mira el dibujo. De repente, las relaciones se vuelven obvias. Verás triángulos rectángulos donde antes no los veías. Notarás si una pendiente es positiva o negativa. Podrás estimar la respuesta antes de escribir una sola ecuación.

Este método te calma, te centra y te da una hoja de ruta visual. Es tu ancla en la tormenta del examen.

El Arsenal Esencial: Las 3 Fórmulas que son el 80% de tu Examen

No necesitas 50 fórmulas. Necesitas dominar tres. Son tus navajas suizas.

1. Distancia entre Dos Puntos: El Metro del Plano Cartesiano

• La Misión: Calcular la longitud de un segmento de recta entre dos puntos P1​(x1​,y1​) y P2​(x2​,y2​).
• La Fórmula: \(d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\)​
• La Estrategia Bajo Presión: ¡No te asustes! Esto no es más que el Teorema de Pitágoras disfrazado. El término \((x_2 - x_1)\) es la base de un triángulo rectángulo y \((y_2​−y_1​)\) es la altura. Estás calculando la hipotenusa. Si dibujas los puntos, lo verás inmediatamente.

2. Punto Medio: El Centro de Todo

• La Misión: Encontrar las coordenadas exactas del punto medio de un segmento.
• La Fórmula: \(P_m = \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2} \right)\)
• La Estrategia Bajo Presión: Piensa en esto como sacar un "promedio". Es el promedio de las 'x' y el promedio de las 'y'. Es simple, rápido y muy común en problemas de circunferencias donde te dan el diámetro y necesitas el centro.

3. Pendiente de una Recta: La Inclinación del Éxito

• La Misión: Medir la inclinación de una recta. Es el concepto más importante.
• La Fórmula: \(m = \frac{y_2 - y_1}{x_2 - x_1} = \frac{\text{elevación}}{\text{avance}}\)​
• La Estrategia Bajo Presión:
  • Visualiza: Pendiente positiva (/) sube de izquierda a derecha. Pendiente negativa (\) baja. Pendiente cero (—) es horizontal. Pendiente indefinida (|) es vertical. Un simple vistazo a tu dibujo te permite verificar si el signo de tu resultado es correcto.
  • Atajo Mortal: Si te dan la ecuación general de la recta Ax+By+C=0, la pendiente es \(m = -A/B\). Este truco te ahorra minutos preciosos de despejar la 'y'. ¡Apréndetelo!

Reactivo Clave #1: La Ecuación de la Recta المستقيم

Este es el pan de cada día en tu examen. Pero todo se simplifica a un principio: para encontrar la ecuación de CUALQUIER recta, solo necesitas dos cosas: un punto \((x_1​,y_1​)\) y la pendiente (m).

Una vez que los tienes, los introduces en la ecuación punto-pendiente y el problema está resuelto:\(y - y_1 = m(x - x_1)\)

El juego consiste en encontrar ese punto y esa pendiente a partir de la información que te dan.

Escenario A: Te dan dos puntos.

1. Encuentra la pendiente (m) usando la fórmula \(m = \frac{y_2 - y_1}{x_2 - x_1}\).
2. Elige uno de los puntos (cualquiera de los dos funciona).
3. Sustituye en la ecuación punto-pendiente y simplifica.

Escenario B: Te dan un punto y una recta paralela o perpendicular.

Esta es la pregunta favorita de los evaluadores para ver si estás atento.

• Rectas Paralelas (||): Tienen la misma pendiente. \(m_1 = m_2\).
• Rectas Perpendiculares (⊥): Sus pendientes son recíprocas y de signo contrario. \(m_2 = -1/m_1\).

Estrategia:

1. Mira la recta que te dan como referencia.
2. Calcula su pendiente (usa el atajo \(m = -A/B\) si está en forma general).
3. Aplica la condición: si es paralela, usa esa misma pendiente. Si es perpendicular, inviértela y cámbiale el signo.
4. Usa el punto que te dieron y tu nueva pendiente en la ecuación punto-pendiente. ¡Listo!

Reactivo Clave #2: La Circunferencia ⭕

No te dejes intimidar por la ecuación general \(x^2 + y^2 + Dx + Ey + F = 0\). Es una distracción. En el corazón de cada circunferencia solo hay dos datos que importan:

Cálculo Diferencial para tu Examen de Admisión a Ingeniería: La Guía Definitiva que tu Competencia NO Quiere que Leas

Aritmética Esencial: 20 Ejercicios Tipo Examen de Admisión Resueltos

1. Su centro: Un punto \((h, k)\).
2. Su radio: Una distancia \(r\).

Si tienes esto, tienes la ecuación ordinaria (o canónica), que es mucho más amigable: \((x - h)^2 + (y - k)^2 = r^2\)

La Misión Más Común: Pasar de la Forma General a la Ordinaria

Te darán la ecuación larga y fea, y te preguntarán por el centro o el radio. Tu misión es "excavar" para encontrar los tesoros \((h, k)\) y \(r\). La herramienta para excavar se llama completar el trinomio cuadrado perfecto (TCP).

El Proceso (Mecánico y Rápido):

Dada: \(x^2 + y^2 + Dx + Ey + F = 0\)

1. Agrupa: \((x^2 + Dx) + (y^2 + Ey) = -F\)
2. Completa: Toma el coeficiente de la 'x' lineal (D), divídelo entre 2 y elévalo al cuadrado. Súmalo en ambos lados. Haz lo mismo para la 'y' (con E).
   • Término para \((\frac{D}{2})^2\)
   • Término para \((\frac{E}{2})^2\)
3. Factoriza: Los paréntesis ahora serán trinomios cuadrados perfectos. \(\left(x + \frac{D}{2}\right)^2 + \left(y + \frac{E}{2}\right)^2 = -F + \left(\frac{D}{2}\right)^2 + \left(\frac{E}{2}\right)^2\)
4. Identifica:
   • El centro es \((h, k) = (-\frac{D}{2}, -\frac{E}{2})\). ¡Ojo con el cambio de signo!
   • El radio al cuadrado es todo lo que está a la derecha de la igualdad. Sácale la raíz cuadrada para encontrar \(r\).

Exam Hack ⚡: A veces, es más rápido tomar las opciones de respuesta (que suelen ser las coordenadas del centro) y ver cuál encaja en la ecuación general que hacer todo el proceso algebraico.

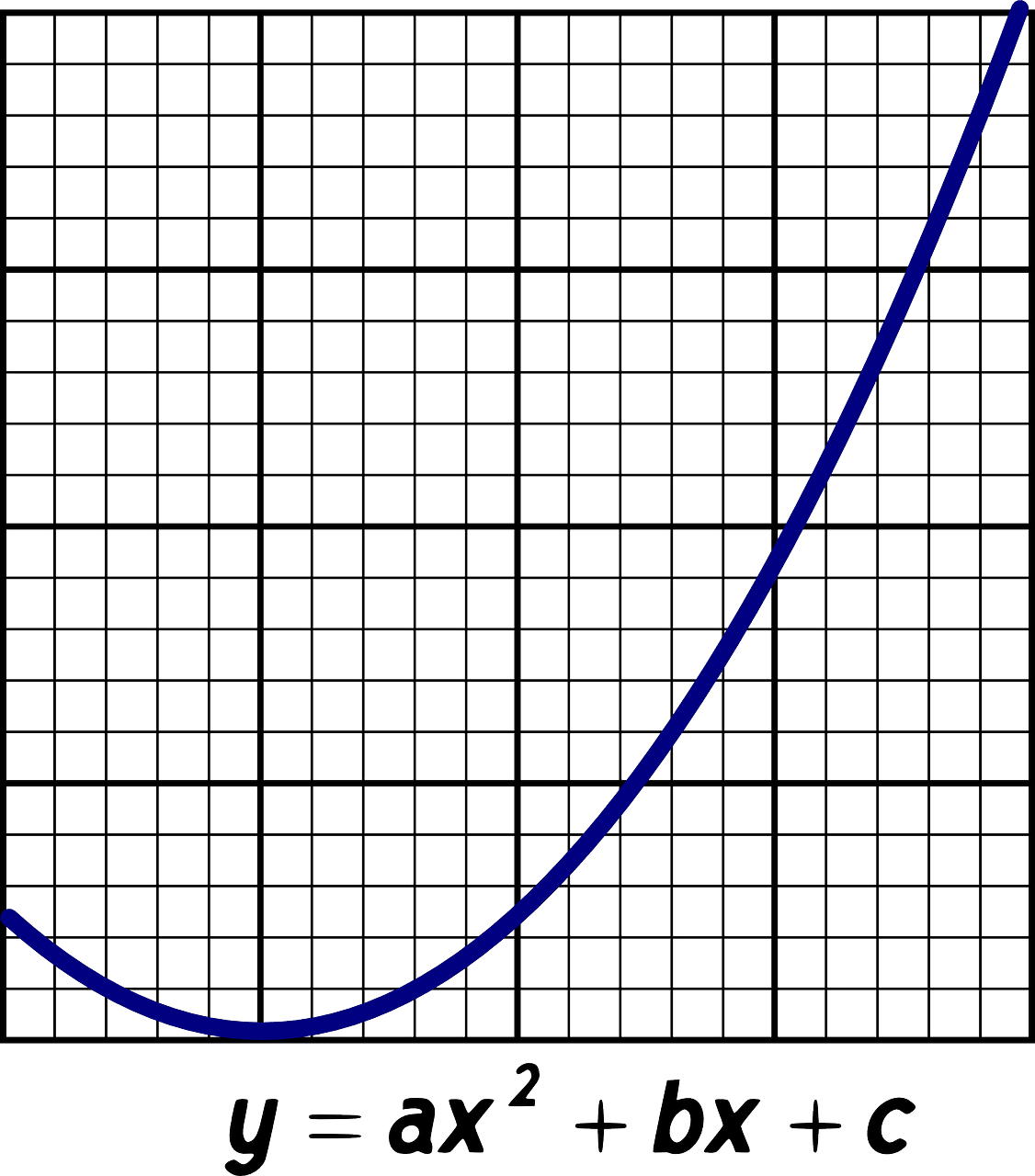
Reactivo Clave #3: La Parábola

Las parábolas parecen complicadas, pero solo hay dos tipos básicos que debes dominar para tu examen.

La Clave: Mira qué variable está elevada al cuadrado.

1. Si la x está al cuadrado → Parábola Vertical.
   • Ecuación: \((x - h)^2 = 4p(y - k)\)
   • Abre hacia arriba si el parámetro p > 0.
   • Abre hacia abajo si p < 0.
2. Si la y está al cuadrado → Parábola Horizontal.
   • Ecuación: \((y - k)^2 = 4p(x - h)\)
   • Abre hacia la derecha si p > 0.
   • Abre hacia la izquierda si p < 0.

Tu Estrategia Bajo Presión:

Cálculo Diferencial para tu Examen de Admisión a Ingeniería: La Guía Definitiva que tu Competencia NO Quiere que Leas

Aritmética Esencial: 20 Ejercicios Tipo Examen de Admisión Resueltos

¿Viene "Funciones y Ecuaciones" en tu examen? Domínalo con esta guía.

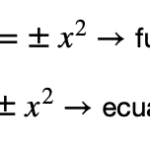
1. Identifica el tipo: Mira la variable al cuadrado para saber si es vertical u horizontal. Esto ya te permite eliminar 2 o 3 opciones de respuesta.
2. Encuentra el Vértice \((h, k)\): Es el punto que acompaña a 'x' y 'y' en los binomios, ¡recuerda siempre cambiarles el signo!
3. Encuentra 'p': El número que multiplica al binomio lineal es igual a 4p. Despeja 'p' para saber cuánto y hacia dónde abre. El parámetro 'p' es la distancia del vértice al foco y del vértice a la directriz.
4. Dibuja: Un simple boceto con el vértice y la dirección de apertura te dará una claridad inmensa y te ayudará a ubicar el foco y la directriz sin dudar.

Estrategias Finales: Cómo Ganarle al Examen

• Usa las Respuestas a tu Favor: En un examen de opción múltiple, las respuestas son parte de la pregunta. Si te piden la ecuación de una recta que pasa por (2, 5), sustituye x=2 y y=5 en las opciones. La que cumpla la igualdad es la correcta. ¡Esto puede ser más rápido que todo el procedimiento!
• Estima y Descarta: Tu dibujo es tu mejor amigo. Si calculas una pendiente y te da positiva, pero tu dibujo claramente muestra una recta que baja, sabes que cometiste un error. Si buscas una distancia y te da 50, pero en tu dibujo los puntos están muy cerca, revisa tus cálculos. Descarta respuestas ilógicas.
• No te Ahogues: ¿Un problema se ve monstruosamente largo o es de un tema que no dominas (ej. hipérbola)? ¡No es una afrenta a tu honor! Márcalo, sáltatelo y vuelve al final si te queda tiempo. Es mejor asegurar 5 preguntas fáciles que perder 10 minutos en una difícil.

Conclusión: Eres un Estratega, no una Calculadora porque ahora ya sabes cómo Resolver Problemas de Geometría Analítica en tu examen de admisión

Resolver problemas de geometría analítica bajo presión no se trata de tener un cerebro sobrehumano. Se trata de tener un sistema.

1. Confía en tu dibujo.
2. Domina tu pequeño arsenal de fórmulas.
3. Identifica el tipo de problema y activa el protocolo correcto.
4. Usa los atajos y las propias respuestas para ganar tiempo.

Practica este enfoque. Haz simulacros de examen cronometrados. Convierte estas estrategias en un reflejo. Cuando llegue el día de la prueba, no verás un problema de geometría y sentirás pánico. Verás un rompecabezas familiar, tomarás tu lápiz y dirás con total confianza: "Yo sé cómo se resuelve esto".

Si quieres conocer otros artículos parecidos a Cómo Resolver Problemas de Geometría Analítica Bajo Presión en tu Prueba de Selección puedes visitar la categoría Guías de Examen de Admisión.